The BIP-39 specification mainly describes the algorithm and process for generating deterministic wallets based on mnemonic (a set of easy-to-remember words).

The specification consists of two main parts:

1. How to generate the mnemonic.
2. How to transform the generated mnemonic into a binary seed.

The following is a look at how to generate deterministic wallets by first describing each of these two parts.

Generating a mnemonic

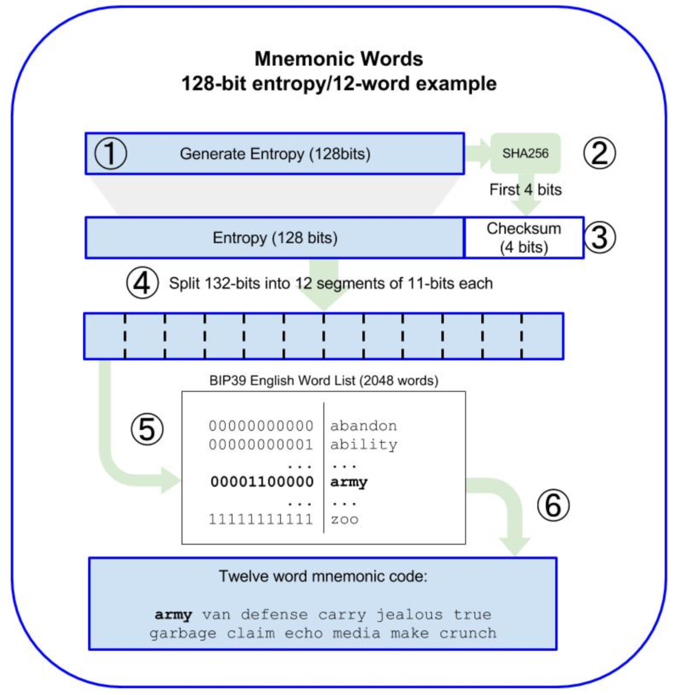
The algorithmic process for generating a mnemonic is as follows：

The process is as follows：

1. Create a random sequence (entropy) of 128 to 256 bits (step size 32 bits)
2. Perform SHA256 on the random sequence generated in the previous step to generate a Hash value, and take the first N bits of the Hash value (entropy length/32, e.g., 128 bits, then N = 4) as the Checksum of the random sequence.
3. Add Checksum to the end of the random sequence generated in the first step, so that for the example in the figure the random sequence with Checksum is 128 + 4 = 132 bits.
4. Separate the random sequence from the previous step by 11-bit segments (split), so that for a sequence of 128-bit entropy length, 12 segments are generated (132/11=12).
5. at this point mapping each value containing an 11-bit segment to a predefined dictionary of 2048 words.
6. The final group of words generated in the order of the cut is the mnemonic.

Seed generation from mnemonics

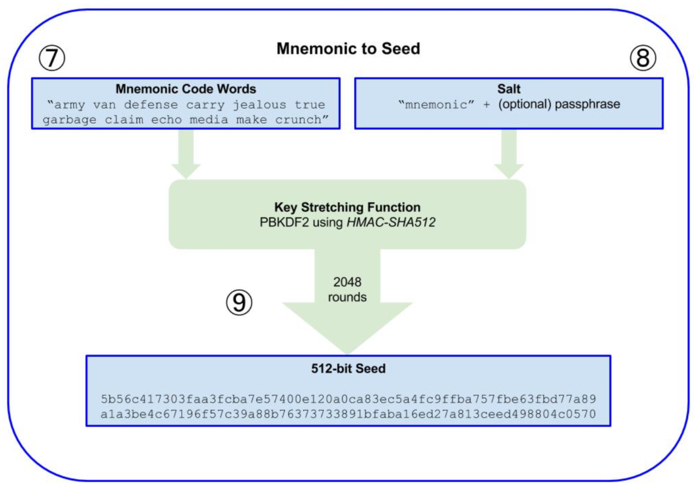
After the mnemonic generation we can generate the seed by using the key generation function PBKDF2 algorithm.

PBKDF2 requires two parameters: a mnemonic and a salt. The purpose of salt is to make cracking more difficult, and in BIP-39 we can introduce passphrase as an additional security factor to protect the seeds.

“PBKDF2 is part of RSA Laboratories' Public-Key Cryptography Standards (PKCS) series,
specifically PKCS #5 v2.0, also published as Internet Engineering Task Force's RFC 2898.”

Following the above mnemonic generation, the following diagram shows the algorithm for seed generation.

• The first parameter of PBKDF2 is the mnemonic generated above.
• The second parameter of PBKDF2 is the salt, which generally consists of a string and an optional concatenation of user-supplied cipher strings.
• PBKDF2 uses the HMAC-SHA512 algorithm, which uses 2048 hashes to produce a 512-bit value as a seed.

Generate HD wallet from seed

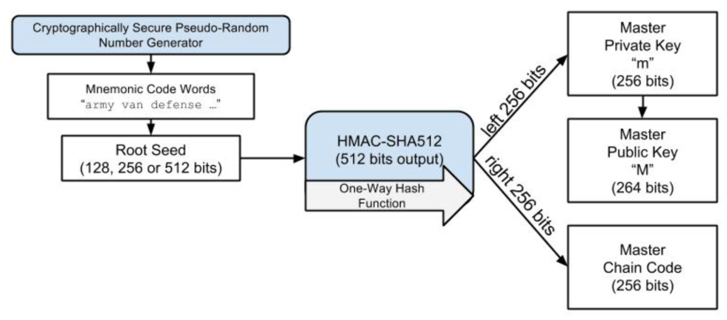
The seed generated above will be used as the root seed of the HD wallet, and the root seed of any HD wallet can recreate the entire HD wallet.

Inputting the root seed into the HMAC-SHA512 algorithm yields a 512-bit hash, the left 256 bits of which are used as the Master Private Key and the right 256 bits as the Master Chain Code. After that, the Master Public Key (264 bits) can be generated by the Master Private Key m.

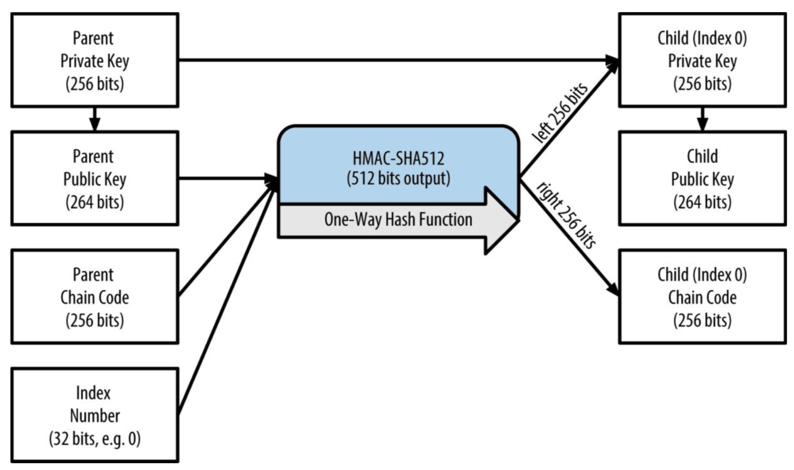
As you can see from the above figure, the HD key is generated with the following parameters.

• Parent Private Key or Parent Public Key; (both are uncompressed 256 bits ECDSA keys).
• Parent Chain Code of 256 bits.
• A 32-bit integer index number.

In addition, the above process is recursive and the Child Private Key in the diagram can be used as the Parent Private Key at the next level.

By entering (Parent Publick Key, Parent Chain Code, Index Number) into the HMAC-SHA512 algorithm, we can generate its subkeys, and we can adjust the Index Number to generate multiple subkeys at the same level.

About Extended Key

Because this key derivation function is unidirectional, all subkeys cannot be used to derive their parent keys or sister keys at the same level, only the parent key and the parent chain code (which are generated from the Parent's Parent level key and chain code) can be used to derive all subkeys and subchain codes, and subsequently generate the corresponding subpublic keys and addresses for signing transactions.

The combination of the Key and Chain Code is called extended key, and the extended key can be used to generate all branches from there on down.

The key provided in the extended key can be either a private key or a public key, combined with the chain code called extended private key and extended public key, respectively, and noted as (k, c) and (K, c), respectively, where the public key K = point(k).

We can derive the extended public key from the extended private key and not vice versa, so for some transaction scenarios (e.g., e-commerce), a new public key and address can be generated for each transaction to receive payment, while the extended private key can be stored in a paper wallet or a hardware wallet for secure offline signing of transactions. As we can see, the security of the extended public key is relatively high, and the following diagram shows the transmission mechanism of the extended parent public key to derive the child private key and generate the child public key: